Todo lo que necesitas saber sobre fracciones: teoría y ejemplos

¿Quieres dominar las fracciones teoria de una vez por todas? ¡No busques más! En este artículo te revelaré los secretos mejor guardados para entender y resolver cualquier problema de fracciones. ¡Deslumbrarás a tus amigos con tus nuevas habilidades matemáticas! ¡Aprende la fracciones teoria de manera fácil y divertida aquí!

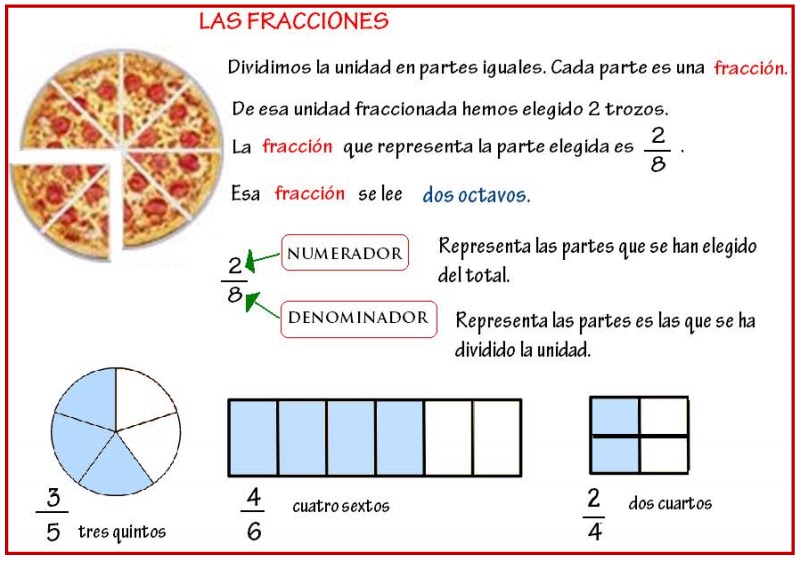
Teoria de fracciones: Descubre la clave detrás de los numeros

Las fracciones son un concepto fundamental en matemáticas y su comprensión es esencial para una variedad de situaciones cotidianas, desde la cocina hasta la construcción. En esta teoría, exploraremos las fracciones con más detalle y descubriremos la clave detrás de los números.

¿Qué son las fracciones?

Las fracciones son una manera de expresar números que representan una parte de un todo. En otras palabras, las fracciones se utilizan para representar una cantidad que es menor que un número entero. Las fracciones se componen de dos partes: el numerador y el denominador.

• El numerador representa la cantidad de partes que se están considerando. Por ejemplo, en la fracción 2/5, el numerador es 2, lo que significa que se están considerando dos partes.
• El denominador representa el número total de partes que conforman el todo. En la fracción 2/5, el denominador es 5, lo que significa que el todo se compone de cinco partes en total.

Las fracciones se pueden representar en diferentes formas, incluyendo representaciones gráficas y decimales. Por ejemplo, la fracción 3/4 puede representarse gráficamente como tres cuartos de un círculo, mientras que su representación decimal es 0.75.

Operaciones con fracciones

Una vez que se comprende la representación de las fracciones, es posible realizar operaciones matemáticas con ellas. Las operaciones comunes incluyen la suma, la resta, la multiplicación y la división.

• Para sumar o restar fracciones, es necesario que tengan el mismo denominador. Si no es así, es necesario encontrar un denominador común antes de realizar la operación.
• Para multiplicar fracciones, se multiplican los numeradores entre sí y los denominadores entre sí.
• Para dividir fracciones, se invierte la segunda fracción (se cambia el numerador y el denominador) y luego se multiplica la primera fracción por la segunda.

Aplicaciones de las fracciones

Las fracciones tienen una amplia variedad de aplicaciones en la vida cotidiana. Algunos ejemplos comunes incluyen:

• En la cocina, las fracciones se utilizan para medir y ajustar las cantidades de los ingredientes en las recetas.
• En la construcción y la carpintería, las fracciones se utilizan para medir y cortar materiales de manera precisa.
• En las finanzas, las fracciones se utilizan para calcular porcentajes y tasas de interés.

Con una comprensión sólida de las fracciones y sus operaciones matemáticas, es posible aplicarlas en una variedad de situaciones cotidianas.

Fracciones: ¿Qué son? Resumen breve

Una fracción es una representación numérica que se utiliza para expresar una cantidad que es una parte de un todo. La fracción se compone de dos números, separados por una línea horizontal llamada barra de fracción.

El número de arriba se llama numerador y representa la cantidad que se está considerando. El número de abajo se llama denominador y representa el total de partes en que se divide el todo.

Por ejemplo, si tenemos una pizza entera y la dividimos en 8 partes iguales, cada una de esas partes representa 1/8 (un octavo) de la pizza. En este caso, el numerador es 1 y el denominador es 8.

Las fracciones se utilizan en muchas situaciones cotidianas, como en la cocina para medir ingredientes, en la carpintería para medir cortes de madera, en las finanzas para calcular porcentajes, entre otros.

Tipos de fracciones

• Fracciones propias: Son aquellas en las que el numerador es menor que el denominador, es decir, representan una cantidad menor que el total. Por ejemplo, 2/5.
• Fracciones impropias: Son aquellas en las que el numerador es mayor o igual que el denominador, es decir, representan una cantidad igual o mayor que el total. Por ejemplo, 7/4.
• Fracciones mixtas: Son aquellas que se componen de un número entero y una fracción propia. Por ejemplo, 3 1/2.

Operaciones con fracciones

Las fracciones se pueden sumar, restar, multiplicar y dividir siguiendo algunas reglas.

• Para sumar o restar fracciones con el mismo denominador, se suman o restan los numeradores y se mantiene el denominador. Por ejemplo, 1/4 + 3/4 = 4/4 = 1.
• Para sumar o restar fracciones con denominadores diferentes, se deben buscar fracciones equivalentes con el mismo denominador. Por ejemplo, 1/3 + 1/4 = 4/12 + 3/12 = 7/12.
• Para multiplicar fracciones, se multiplican los numeradores y los denominadores. Por ejemplo, 1/3 x 2/5 = 2/15.
• Para dividir fracciones, se multiplican la primera fracción por la inversa de la segunda. Por ejemplo, 1/3 ÷ 2/5 = 1/3 x 5/2 = 5/6.

Ahora que conoces qué son las fracciones, los tipos que existen y cómo se pueden operar, podrás utilizarlas para resolver muchos problemas matemáticos y aplicarlos en situaciones cotidianas.

Fracciones: ¿Qué son y cómo se dividen?

Las fracciones son una parte fundamental de las matemáticas y se utilizan para representar números que no son enteros. Básicamente, una fracción es una división de dos números enteros, donde el número de arriba se llama numerador y el número de abajo se llama denominador.

Por ejemplo, la fracción 2/3 representa la división de 2 entre 3. En esta fracción, el numerador es 2 y el denominador es 3.

Tipos de fracciones

Existen varios tipos de fracciones, entre las más comunes se encuentran:

• Fracciones propias: Son aquellas en las que el numerador es menor que el denominador. Por ejemplo, 1/4.
• Fracciones impropias: Son aquellas en las que el numerador es mayor o igual que el denominador. Por ejemplo, 7/4.
• Fracciones mixtas: Son aquellas que incluyen un número entero y una fracción propia. Por ejemplo, 1 1/2.

División de fracciones

Para dividir fracciones, se debe multiplicar la primera fracción por la inversa de la segunda fracción. Es decir, si queremos dividir la fracción 2/3 entre la fracción 4/5, debemos multiplicar 2/3 por 5/4.

El resultado de esta operación sería:

2/3 ÷ 4/5 = 2/3 x 5/4 = 10/12

Este resultado puede simplificarse dividiendo tanto el numerador como el denominador por su máximo común divisor. En este caso, el máximo común divisor de 10 y 12 es 2, por lo que podemos simplificar la fracción dividiendo ambos números por 2:

10/12 = 5/6

Resuelve fracciones fácilmente: Guía paso a paso

Las fracciones son una parte fundamental de las matemáticas. Sin embargo, a pesar de que son una herramienta útil, pueden ser un dolor de cabeza para muchos estudiantes. Si eres uno de ellos, no te preocupes. Con esta guía paso a paso, podrás resolver fracciones fácilmente y sin estrés.

Paso 1: Identifica el numerador y el denominador

Una fracción se compone de dos partes: el numerador y el denominador. El numerador es el número de arriba y el denominador es el número de abajo. Por ejemplo, en la fracción 3/4, el numerador es 3 y el denominador es 4.

Paso 2: Convierte a un denominador común

Para sumar o restar fracciones, necesitas tener un denominador común. Para hacer esto, primero debes identificar el denominador y luego convertirlo a un número que sea común a todas las fracciones que estás sumando o restando. Por ejemplo, si quieres sumar 1/2 y 1/4, debes convertir 1/2 a 2/4 y luego sumar:

• 1/2 = 2/4
• 1/4
• ——-
• 3/4

Paso 3: Multiplica los numeradores y los denominadores

Para multiplicar fracciones, simplemente multiplica los numeradores y luego los denominadores. Por ejemplo, para multiplicar 1/2 por 2/3:

• 1/2 x 2/3 = (1 x 2) / (2 x 3) = 2/6

Paso 4: Simplifica la fracción

Para simplificar una fracción, divide el numerador y el denominador por el mismo número. Por ejemplo, para simplificar 4/8:

• 4/8 = (4 ÷ 4) / (8 ÷ 4) = 1/2

Con estos cuatro pasos básicos, podrás resolver fracciones fácilmente en cualquier problema de matemáticas que se te presente. ¡Buena suerte!

las fracciones son una herramienta matemática fundamental en nuestra vida diaria y en muchos campos profesionales. A través de su comprensión y manipulación, podemos resolver problemas complejos, hacer cálculos precisos y tomar decisiones informadas en diversas situaciones. Esperamos que este artículo haya sido útil para mejorar tu comprensión de la teoría detrás de las fracciones y cómo aplicarla en tu vida cotidiana. ¡Sigue aprendiendo y practicando!

Este contenido también puede ser encontrado cuando buscas Fracciones teoria

Ana Belén López

Ana Belén López es una educadora con experiencia en la enseñanza en diferentes niveles educativos. Ha trabajado en proyectos de investigación en el campo de la pedagogía y la didáctica. Sus principales intereses de investigación incluyen la educación inclusiva, el uso de tecnología en el aula y la educación en valores.

teoriaonline.com