Teoría de la circunferencia trigonométrica: todo lo que necesitas saber
¡Descubre todo lo que necesitas saber sobre la Circunferencia Trigonométrica Teoría en este artículo imprescindible! Si estás buscando entender la teoría detrás de este importante concepto matemático, estás en el lugar correcto. Aprenderás todo lo que necesitas saber sobre la circunferencia unitaria, ángulos y coordenadas polares. No te pierdas esta guía completa sobre la Circunferencia Trigonométrica Teoría y conviértete en un experto en la materia. ¡Sigue leyendo!
Funciones trigonométricas en la circunferencia unitaria: guía completa
Funciones trigonométricas en la circunferencia unitaria: guía completa
La circunferencia unitaria es una herramienta muy útil para comprender las funciones trigonométricas. En este artículo, exploraremos en detalle las funciones trigonométricas en la circunferencia unitaria, su definición y cómo utilizarlas.
Definición de la circunferencia unitaria
La circunferencia unitaria es una circunferencia que tiene un radio de 1 unidad y está centrada en el origen del plano cartesiano. En otras palabras, su ecuación es x² + y² = 1. La circunferencia unitaria es importante porque nos permite visualizar las funciones trigonométricas como relaciones entre los ángulos y las coordenadas de los puntos en la circunferencia.
Funciones trigonométricas en la circunferencia unitaria
Hay cuatro funciones trigonométricas principales: el seno, el coseno, la tangente y la cotangente. Estas funciones son relaciones entre los ángulos y las coordenadas de los puntos en la circunferencia unitaria.
Seno
El seno de un ángulo se define como la coordenada y del punto en la circunferencia unitaria que forma ese ángulo con el eje x. La función seno se representa como sin(θ).
Coseno
El coseno de un ángulo se define como la coordenada x del punto en la circunferencia unitaria que forma ese ángulo con el eje x. La función coseno se representa como cos(θ).
Tangente
La tangente de un ángulo se define como la coordenada y dividida por la coordenada x del punto en la circunferencia unitaria que forma ese ángulo con el eje x. La función tangente se representa como tan(θ).
Cotangente
La cotangente de un ángulo se define como la coordenada x dividida por la coordenada y del punto en la circunferencia unitaria que forma ese ángulo con el eje x. La función cotangente se representa como cot(θ).
Usando las funciones trigonométricas
Las funciones trigonométricas se utilizan en muchas áreas, como la física y la ingeniería. Por ejemplo, el seno y el coseno se utilizan para modelar el movimiento armónico simple, mientras que la tangente y la cotangente se utilizan para calcular la pendiente de una línea.
Utiliza esta guía completa para comprender mejor estas funciones y cómo aplicarlas en diversos campos.
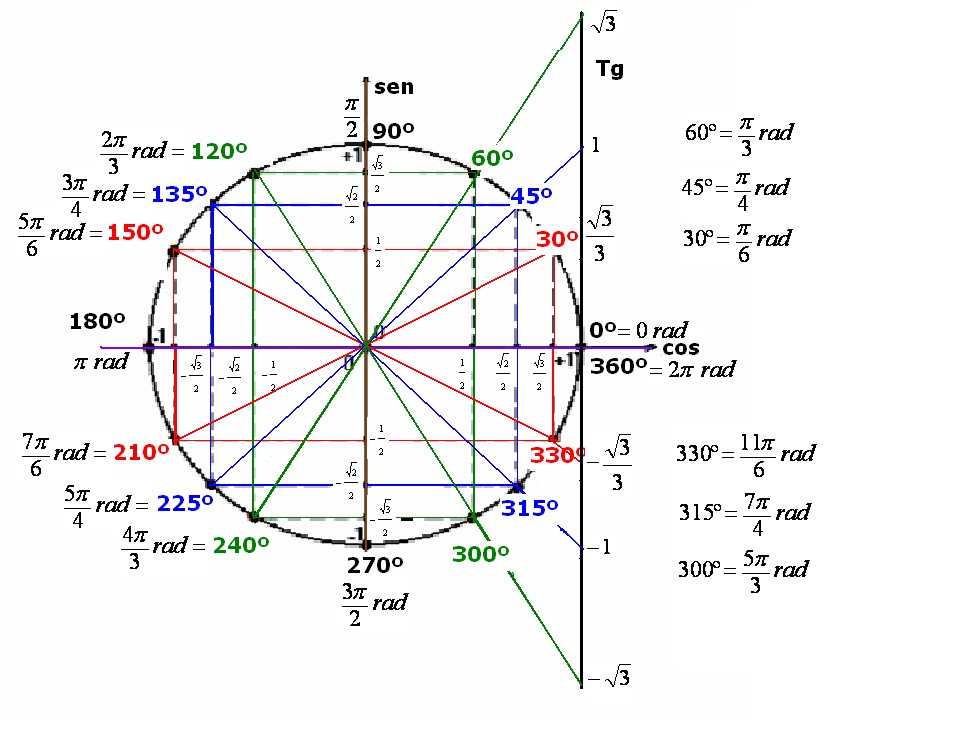
Cuadrantes en Circunferencia Trigonométrica: Guía Completa
En trigonometría, la circunferencia trigonométrica es una herramienta esencial que nos permite comprender mejor las funciones trigonométricas y sus propiedades. En esta guía completa, nos enfocaremos en los cuadrantes de la circunferencia trigonométrica y cómo estos nos ayudan a resolver problemas trigonométricos.
¿Qué es la circunferencia trigonométrica?
La circunferencia trigonométrica es una circunferencia con centro en el origen de un sistema de coordenadas cartesianas. Esta circunferencia se utiliza para representar las funciones trigonométricas seno, coseno y tangente de un ángulo.
La circunferencia trigonométrica se divide en cuatro partes iguales que se conocen como cuadrantes. Cada cuadrante tiene un ángulo central que es de 90 grados o π/2 radianes. Los cuadrantes están numerados en sentido antihorario y se identifican con los números romanos I, II, III y IV.
¿Cómo se identifican los cuadrantes?
Para identificar los cuadrantes en la circunferencia trigonométrica, se utiliza el signo del valor de las funciones trigonométricas en cada cuadrante. A continuación, se presenta una tabla con el signo de las funciones trigonométricas en cada cuadrante:
- Cuadrante I: todas las funciones trigonométricas son positivas.
- Cuadrante II: el seno es positivo, el coseno es negativo y la tangente es negativa.
- Cuadrante III: el seno y la tangente son negativos, el coseno es positivo.
- Cuadrante IV: el seno es negativo, el coseno y la tangente son positivos.
Es importante comprender cómo identificar los cuadrantes para poder resolver problemas trigonométricos de manera efectiva.
Inventor de la trigonometría: Descubre quién creó los cálculos trigonométricos
La trigonometría es una rama de las matemáticas que se encarga de estudiar las relaciones entre los ángulos y los lados de un triángulo. Esta disciplina es de gran importancia en muchas áreas del conocimiento, como la física, la astronomía, la cartografía, la arquitectura, la ingeniería, entre otras.
La historia de la trigonometría se remonta a la antigua Mesopotamia y Egipto, donde se utilizaban técnicas geométricas para medir terrenos y construcciones. Sin embargo, el desarrollo de la trigonometría tal como la conocemos hoy en día se atribuye a los matemáticos griegos.
La circunferencia trigonométrica
Uno de los conceptos fundamentales de la trigonometría es la circunferencia trigonométrica. Esta es una circunferencia de radio unitario (es decir, de longitud igual a uno), que se utiliza para representar gráficamente las funciones trigonométricas seno y coseno.
La circunferencia se divide en 360 grados, y cada grado se subdivide en 60 minutos y cada minuto en 60 segundos. De esta manera, se puede medir cualquier ángulo en términos de grados, minutos y segundos.
La idea de utilizar la circunferencia para representar las funciones trigonométricas se atribuye al matemático suizo Leonhard Euler, quien vivió en el siglo XVIII. Sin embargo, los cálculos trigonométricos ya se conocían desde mucho antes.
El inventor de la trigonometría
El mérito de haber creado los cálculos trigonométricos se atribuye al matemático griego Hiparco de Nicea, quien vivió en el siglo II a.C. Hiparco era un astrónomo y geógrafo que comenzó a utilizar las funciones trigonométricas para resolver problemas de medición y cálculo de distancias en la Tierra y en el espacio.
Entre las contribuciones de Hiparco a la trigonometría se encuentran la creación de la tabla de cuerdas, que relaciona los ángulos con las longitudes de los segmentos de una cuerda que se extiende sobre la circunferencia; y la introducción de los conceptos de seno y coseno, que se utilizan para calcular las longitudes de los lados de un triángulo rectángulo.
La trigonometría de Hiparco se basaba en la geometría, y no utilizaba las funciones trigonométricas tal como las conocemos hoy en día. Estos cálculos fueron perfeccionados por otros matemáticos griegos, como Ptolomeo y Euclides, y más tarde por los matemáticos árabes y europeos de la Edad Media.
Conclusiones
La circunferencia trigonométrica es una herramienta fundamental para representar gráficamente las funciones trigonométricas seno y coseno. El inventor de los cálculos trigonométricos fue Hiparco de Nicea, quien vivió en el siglo II a.C. y utilizó estos cálculos para resolver problemas en astronomía y geografía. La trigonometría de Hiparco sentó las bases para el desarrollo posterior de esta disciplina, que llegó a su forma actual gracias a los aportes de muchos otros matemáticos a lo largo de la historia.
La trigonometría es una rama de las matemáticas que se encarga de estudiar las relaciones entre los ángulos y los lados de un triángulo. Las razones trigonométricas son las relaciones que existen entre los lados de un triángulo rectángulo y sus ángulos. Estas razones son utilizadas para resolver problemas en diferentes campos como la física, la ingeniería, la arquitectura y la navegación.
La circunferencia es una línea curva cerrada en la que todos los puntos están a la misma distancia del centro. La circunferencia trigonométrica es una herramienta utilizada en trigonometría para estudiar las razones trigonométricas de un ángulo. La circunferencia trigonométrica es una circunferencia de radio 1 que se coloca en un sistema de coordenadas cartesianas.
En la circunferencia trigonométrica, el ángulo se mide en sentido contrario a las agujas del reloj desde el punto (1,0) sobre el eje x. El punto donde el ángulo intersecta la circunferencia se denomina punto terminal. La coordenada x del punto terminal es la razón trigonométrica del coseno del ángulo y la coordenada y es la razón trigonométrica del seno del ángulo.
Las Razones Trigonométricas
Las razones trigonométricas más comunes son el seno, el coseno y la tangente. La siguiente lista describe cada una de estas razones:
- Seno: El seno de un ángulo es igual a la longitud del cateto opuesto dividido por la longitud de la hipotenusa.
- Coseno: El coseno de un ángulo es igual a la longitud del cateto adyacente dividido por la longitud de la hipotenusa.
- Tangente: La tangente de un ángulo es igual a la longitud del cateto opuesto dividido por la longitud del cateto adyacente.
Estas razones pueden ser representadas en la circunferencia trigonométrica. El seno del ángulo está representado por la coordenada y del punto terminal, el coseno del ángulo está representado por la coordenada x del punto terminal y la tangente del ángulo está representada por la pendiente de la recta que pasa por el origen y el punto terminal.
Usos de la Circunferencia Trigonométrica
La circunferencia trigonométrica permite calcular las razones trigonométricas de cualquier ángulo, no solo de los ángulos de un triángulo rectángulo. Además, permite visualizar de manera gráfica las razones trigonométricas y facilita la comprensión de los conceptos de la trigonometría.
La circunferencia trigonométrica también se utiliza para resolver ecuaciones trigonométricas y para representar funciones trigonométricas. La representación gráfica de una función trigonométrica es conocida como gráfica trigonométrica y se obtiene a partir de la circunferencia trigonométrica.
la circunferencia trigonométrica es una herramienta crucial en la resolución de problemas matemáticos que involucran ángulos y funciones trigonométricas. A través de su comprensión, podemos simplificar y visualizar conceptos complejos para su aplicación en diversas áreas de la ciencia y la tecnología. conocer y dominar la teoría de la circunferencia trigonométrica es fundamental para cualquier estudiante o profesional que se dedique a las matemáticas y sus aplicaciones en la vida real.
Este contenido también puede ser encontrado cuando buscas Circunferencia trigonometrica teoria
TeoriaOnline.com cuenta con un equipo de trabajo al cual llamamos cariñosamente «Teoria Online Team» este es un equipo de trabajo conformado por expertos en distintas áreas del conocimiento, incluyendo filosofía, historia, ciencia, educación, arte, política, psicología, religión, sociedad y evolución, entre otras.
También te puede interesar
Teoría Corpuscular: La explicación científica que debes conocer
Descubre la Teoría del Microbio: La clave para entender la salud y la enfermedad
Descubre la Teoría de Máquinas y Mecanismos: Todo lo que necesitas saber
Descubre la Teoría Glacial: El Origen de los Glaciares
Descubre la teoría de bandas en el enlace metálico: una explicación completa
Descubre la Teoría del Caos de Lorenz: El caos que rige el universo
5 Comentarios
Los comentarios están cerrados.
¡Qué locura de teoría! Nunca pensé que una circunferencia podría ser tan interesante.
¡Vaya, vaya! Parece que no te has dado cuenta de lo fascinante que puede ser el mundo de las matemáticas. La geometría tiene mucho más que ofrecer que solo líneas rectas. Abre tu mente, amigo, y descubrirás un universo de maravillas.
No entiendo para qué sirve la circunferencia trigonométrica, ¡mejor me quedo con la calculadora!
La circunferencia trigonométrica es fundamental para comprender las relaciones entre ángulos y funciones trigonométricas. No subestimes su utilidad, te ayudará a entender los conceptos en lugar de depender únicamente de una calculadora. ¡Explora y descubre nuevas perspectivas!
¡Vaya, la teoría de la circunferencia trigonométrica suena complicada pero interesante! ¿Alguien más se siente así?