La conexión esencial entre teoría de conjuntos, lógica matemática y álgebra booleana
¿Quieres descubrir cómo la relación entre teoría de conjuntos, lógica matemática y álgebra booleana puede ayudarte a resolver problemas complejos? En este artículo te lo explicaremos todo de manera clara y concisa. Toma asiento y prepárate para expandir tus conocimientos en matemáticas y lógica. ¡No te lo pierdas!
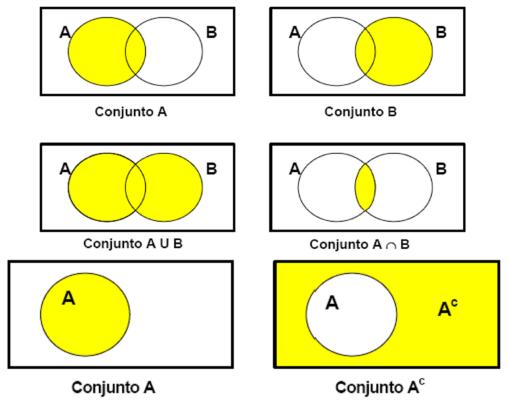
Conexión entre la teoría de conjuntos y álgebra
La teoría de conjuntos, la lógica matemática y el álgebra booleana están estrechamente relacionados entre sí, y su conexión se basa en el uso común de los conjuntos.
Teoría de conjuntos
La teoría de conjuntos es una rama de las matemáticas que estudia la colección de objetos llamados conjuntos y las operaciones que se pueden realizar con ellos. Los conjuntos son una herramienta fundamental en la matemática moderna.
Lógica matemática
La lógica matemática es el estudio de los principios y métodos utilizados para distinguir el razonamiento correcto del incorrecto. Los conjuntos se utilizan en la lógica matemática para representar proposiciones y las operaciones que se realizan con ellos son similares a las operaciones booleanas.
Álgebra booleana
El álgebra booleana es una rama de las matemáticas que se ocupa de las operaciones lógicas y aritméticas en los números binarios (0 y 1). Los conjuntos se utilizan en el álgebra booleana para representar las variables lógicas y las operaciones que se realizan con ellos son las mismas que las operaciones conjuntistas.
Conexión entre teoría de conjuntos y álgebra booleana
La conexión entre la teoría de conjuntos y el álgebra booleana se basa en el hecho de que los conjuntos pueden representarse como funciones booleanas. Cada elemento del conjunto se representa por una variable booleana, y la presencia o ausencia de este elemento se representa por los valores 1 y 0, respectivamente. Las operaciones conjuntistas, como la unión, la intersección y la diferencia, se pueden representar mediante operaciones booleanas.
- La unión de dos conjuntos se representa por la operación OR (o inclusivo) en el álgebra booleana.
- La intersección de dos conjuntos se representa por la operación AND (y inclusivo) en el álgebra booleana.
- Conjunto: una colección de elementos que comparten alguna propiedad común.
- Elemento: un objeto que pertenece a

Álgebra Booleana e Informática: Una relación fundamental
La álgebra booleana es una rama de las matemáticas que se centra en el estudio de las operaciones lógicas y los conjuntos. Esta disciplina es fundamental en el campo de la informática, ya que se utiliza para la creación y diseño de circuitos electrónicos, programas informáticos y la realización de operaciones lógicas en general.
La relación entre la teoría de conjuntos, lógica matemática y álgebra booleana
La teoría de conjuntos es una rama de las matemáticas que se ocupa del estudio de los conjuntos y sus propiedades. La lógica matemática, por su parte, es una disciplina que se centra en el estudio de la estructura y las propiedades de los sistemas formales de razonamiento.
La relación entre estas disciplinas y el álgebra booleana radica en que los conjuntos y las operaciones lógicas son los fundamentos sobre los que se construye esta rama de las matemáticas. De hecho, el álgebra booleana se basa en la lógica binaria y las operaciones lógicas AND, OR y NOT.
Aplicaciones de la álgebra booleana en informática
La álgebra booleana es esencial en la electrónica digital y en la creación de circuitos lógicos. Los circuitos digitales se basan en la lógica binaria y las operaciones AND, OR y NOT, que permiten la realización de operaciones lógicas complejas con relativa facilidad.
Además, la álgebra booleana es un elemento fundamental en la programación de sistemas informáticos. La lógica binaria y las operaciones lógicas son la base de los programas informáticos, permitiendo la creación de algoritmos y la toma de decisiones complejas.
Conclusiones
La relación entre la teoría de conjuntos, lógica matemática y álgebra booleana es esencial para entender los fundamentos sobre los que se construyen estas disciplinas y cómo
Teoría de conjuntos: ¿útil en la actualidad?
Teoría de conjuntos: ¿útil en la actualidad? La teoría de conjuntos es una rama de las matemáticas que se encarga del estudio de los conjuntos, sus propiedades y relaciones. Aunque pueda parecer una disciplina abstracta y alejada de la realidad, lo cierto es que su utilidad se extiende a muchas áreas del conocimiento.
Relación entre teoría de conjuntos, lógica matemática y álgebra booleana
La lógica matemática se basa en la utilización de símbolos y reglas matemáticas para el estudio del razonamiento y la argumentación. La teoría de conjuntos es una herramienta esencial en lógica matemática, ya que permite definir y estudiar los conjuntos de objetos y su relación entre ellos.
Por otro lado, el álgebra booleana es una rama de la matemática que estudia las operaciones lógicas sobre variables booleanas, es decir, variables que solo pueden tomar los valores de verdadero o falso. Esta rama también está estrechamente relacionada con la teoría de conjuntos, ya que las operaciones lógicas se pueden entender como operaciones entre conjuntos.
Aplicaciones de la teoría de conjuntos en la actualidad
La utilidad de la teoría de conjuntos se extiende a muchas áreas de la ciencia y la tecnología. Algunas de sus aplicaciones más destacadas son:
- En informática, la teoría de conjuntos es fundamental en el diseño de algoritmos y en la programación de bases de datos.
- En física, la teoría de conjuntos es utilizada en la teoría de los conjuntos y la topología para el estudio de los fundamentos de la mecánica cuántica.
- En estadística, la teoría de conjuntos es utilizada para el estudio de la probabilidad y la teoría de la medida.
- En biología, la teoría de conjuntos es utilizada en la teoría de la complejidad y la teoría de sistemas para el estudio de los sistemas biológicos.Este contenido también puede ser encontrado cuando buscas Relacion entre teoria de conjuntos logica matematica y algebra booleana

Carmen García es antropóloga social y cultural con experiencia en investigación etnográfica en América Latina y África. Sus principales intereses de investigación incluyen las culturas indígenas, la identidad cultural, la migración y el género.
Teoría de conjuntos en la lógica matemática: ¿Qué es?
La teoría de conjuntos es una rama de las matemáticas que se encarga del estudio de los conjuntos y las operaciones que se pueden realizar con ellos. Esta teoría se basa en la idea de que cualquier objeto matemático se puede representar como un conjunto, y que las propiedades de ese objeto están determinadas por las propiedades de ese conjunto.
En la lógica matemática, la teoría de conjuntos es fundamental, ya que proporciona un lenguaje común para expresar las relaciones entre objetos matemáticos. Por ejemplo, se pueden representar las relaciones entre conjuntos utilizando operaciones como la unión, la intersección y la diferencia.
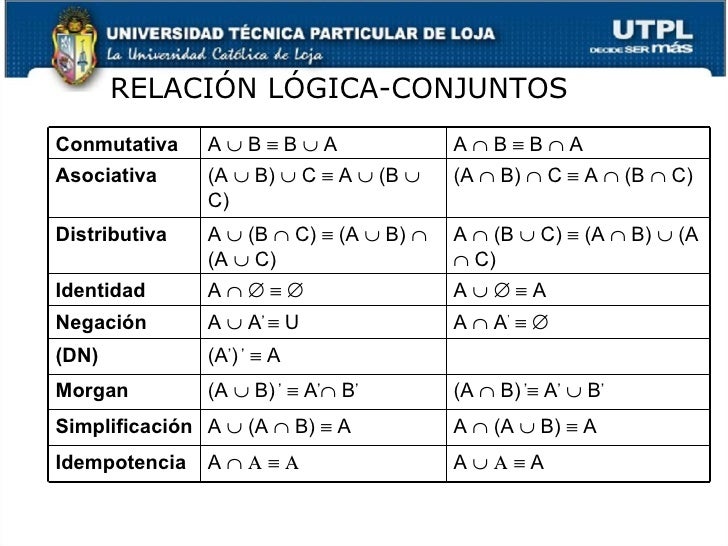
Relación entre la teoría de conjuntos, la lógica matemática y el álgebra booleana
La teoría de conjuntos, la lógica matemática y el álgebra booleana están estrechamente relacionados. En la lógica matemática, se utilizan los conjuntos para representar las proposiciones y las relaciones entre ellas. Por ejemplo, se puede representar la proposición «Todos los perros son animales» como el conjunto de todos los perros, y el conjunto de todos los animales.
El álgebra booleana es un sistema matemático que se basa en los conjuntos y las operaciones booleanas. Esta álgebra se utiliza para el diseño y análisis de circuitos lógicos, y en la programación de computadoras.
Las operaciones booleanas, como la negación, la conjunción y la disyunción, son equivalentes a las operaciones de complemento, intersección y unión en la teoría de conjuntos. Por lo tanto, la teoría de conjuntos es esencial para el estudio de la lógica matemática y el álgebra booleana.
Esta teoría proporciona un lenguaje común para expresar las relaciones entre objetos matemáticos, y se utiliza en muchas áreas de las matemáticas y la informática.
Algunos conceptos clave en la teoría de conjuntos:
También te puede interesar

La Teoría del Todo: Película Completa en Español de Stephen Hawking

La Teoría del Crecimiento Cero: ¿Es posible un futuro sostenible?

La evolución de la teoría del color: desde Newton hasta nuestros días

Descubre cómo la teoría del orden de nacimiento influye en tu personalidad

Descubre la Teoría de la Unión: La clave para entender las relaciones humanas
Descubre la Teoría del Desarrollo Humano de Rosemarie Rizzo Parse
3 Comentarios
Los comentarios están cerrados.


¡Vaya, nunca imaginé que la teoría de conjuntos, la lógica matemática y el álgebra booleana estuvieran tan conectados! ¿Alguien más se sorprende?
¡Vaya, nunca pensé que la teoría de conjuntos, la lógica matemática y el álgebra booleana estuvieran tan conectados! ¿Alguien más sorprendido?
¡Totalmente de acuerdo! Es sorprendente cómo estas disciplinas se entrelazan y complementan entre sí. Es emocionante descubrir las conexiones y aplicaciones que pueden surgir. ¡La belleza de las matemáticas nunca deja de sorprenderme!